--指數 冪
冪(音同「覓」),指乘方運算的結果。nm指將n自乘m次。把nm看作乘方的結果,叫做n的m次冪。
0的0次方是懸而未決的,在某些領域定義為1,某些領域未定義,但並未提出不定義之理由。
重要的恆等式
[編輯]運算法則

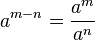
- 如果a ≠ 0,則


[編輯]其他等式
![a^\frac{m}{n} = \sqrt[n]{a^m}](http://upload.wikimedia.org/math/3/6/f/36fd635bf1ff87ecc17fd35882981b3d.png)




- (xm)n = xmn

[編輯]運算律
加法和乘法遵守交換律,比如:2+3 = 5 = 3+2,2×3 = 6 = 3×2,但是冪的運算不遵守交換律,23 = 8,但是32 = 9。
同樣,加法和乘法遵守結合律,比如:(2+3)+4 = 9 = 2+(3+4),(2×3)×4 = 24 = 2×(3×4),冪同樣不遵守:(23)4 = 84 = 4096,但是 。冪的運算順序通常由上到下:
。冪的運算順序通常由上到下:
 。冪的運算順序通常由上到下:
。冪的運算順序通常由上到下:正整數指數冪
表達式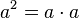 被稱作a的平方,因為邊長為a的正方形面積是a2。
被稱作a的平方,因為邊長為a的正方形面積是a2。
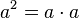 被稱作a的平方,因為邊長為a的正方形面積是a2。
被稱作a的平方,因為邊長為a的正方形面積是a2。表達式 被稱作a的立方,因為邊長為a的正方體面積是a3。
被稱作a的立方,因為邊長為a的正方體面積是a3。
 被稱作a的立方,因為邊長為a的正方體面積是a3。
被稱作a的立方,因為邊長為a的正方體面積是a3。所以32讀作3的平方,23讀作2的立方。
指數表示的是有多少個底數相乘。比如 ,指數是5,底數是3,表示有5個3相乘。
,指數是5,底數是3,表示有5個3相乘。
 ,指數是5,底數是3,表示有5個3相乘。
,指數是5,底數是3,表示有5個3相乘。或者,整數指數冪可以遞歸地定義成:
0的冪
0的正數冪都等於0。
0的負數冪沒有定義。
0的0次方是懸而未決的,在某些領域定義為1,某些領域未定義,但並未提出不定義之理由。
[編輯]負1的冪
-1的奇數冪等於-1
-1的偶數冪等於1
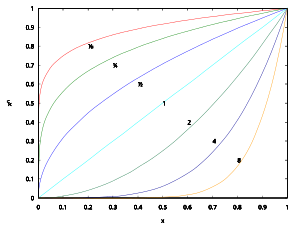
指數非常大時的冪
一個大於1的數的冪趨於無窮大,一個小於-1的數的冪趨於負無窮大
- 當a > 1,
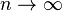 ,
,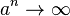
- 當a < − 1,
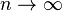 ,
,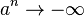
一個絕對值小於1的數的冪趨於0
- 當 | a | < 1,
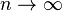 ,
,
1的冪永遠都是1
- 當a = 1,
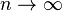 ,
,
如果數a趨於1而它的冪趨於無窮,那麼極限並不一定是上面幾個。一個很重要的例子是:
- 當
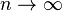 ,
,
N次方根
一個數a的n次方根是x,x使xn = a。
當指數是 時根號上的2可以省略,如:
時根號上的2可以省略,如:![\sqrt{4} = \sqrt[2]{4} = 2](http://upload.wikimedia.org/math/f/f/8/ff80f53840db9709af75f0f5f36014f8.png)
 時根號上的2可以省略,如:
時根號上的2可以省略,如:![\sqrt{4} = \sqrt[2]{4} = 2](http://upload.wikimedia.org/math/f/f/8/ff80f53840db9709af75f0f5f36014f8.png)
[編輯]有理數冪
有理數指數通常可以理解成
[編輯]e的冪
指數函數的定義是:
可以很簡單地證明e的正整數k次方ek是:
[編輯]實數指數冪
因為所有實數可以近似地表示為有理數,任意實數指數x可以定義成:
例如:
於是
實數指數冪通常使用對數來定義,而不是近似有理數。
- b = elnb
根據對數和指數運算的規則:
這就是實數指數冪的定義:
實數指數冪bx的這個定義和上面使用有理數指數和連續性的定義相吻合。對於複數,這種定義更加常用。
[編輯]負實數的實數冪
使用對數和有理數指數都不能將ak(其中a是負實數,k實數)定義成實數。在一些特殊情況下,給出一個定義是可行的:負指數的整數指數冪是實數,有理數指數冪對於 (n是奇數)可以使用n次方根來計算,但是因為沒有實數x使x2 = − 1,對於
(n是奇數)可以使用n次方根來計算,但是因為沒有實數x使x2 = − 1,對於 (n是偶數)時必須使用虛數單位i。
(n是偶數)時必須使用虛數單位i。
 (n是奇數)可以使用n次方根來計算,但是因為沒有實數x使x2 = − 1,對於
(n是奇數)可以使用n次方根來計算,但是因為沒有實數x使x2 = − 1,對於 (n是偶數)時必須使用虛數單位i。
(n是偶數)時必須使用虛數單位i。使用對數的方法不能定義a ≤ 0時的ak為實數。實際上,ex對於任何實數x都是正的,所以ln(a)對於負數沒有意義。
使用有理數指數冪來逼近的方法也不能用於負數a因為它依賴於連續性。函數f(r) = ar對於任何正的有理數a是連續的,但是對於負數a,函數f在有些有理數r上甚至不是連續的。
例如:當a = -1,它的奇數次根等於-1。所以如果n是正奇數整數, 當m是奇數,
當m是奇數, 當m是偶數。雖然有理數q使 − 1q = 1的集合是稠密集,但是有理數q使 − 1q = − 1的集合也是。所以函數 − 1q在有理數體不是連續的。
當m是偶數。雖然有理數q使 − 1q = 1的集合是稠密集,但是有理數q使 − 1q = − 1的集合也是。所以函數 − 1q在有理數體不是連續的。
 當m是奇數,
當m是奇數, 當m是偶數。雖然有理數q使 − 1q = 1的集合是稠密集,但是有理數q使 − 1q = − 1的集合也是。所以函數 − 1q在有理數體不是連續的。
當m是偶數。雖然有理數q使 − 1q = 1的集合是稠密集,但是有理數q使 − 1q = − 1的集合也是。所以函數 − 1q在有理數體不是連續的。

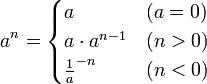
![\sqrt[n]{a}](http://upload.wikimedia.org/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) ,其中
,其中 叫做根號。或者,a的n次方根也可以寫成
叫做根號。或者,a的n次方根也可以寫成 . 例如
. 例如
![a^{\frac{m}{n}} = (a^m)^{\frac{1}{n}} = \sqrt[n]{a^m}](http://upload.wikimedia.org/math/f/b/8/fb8781d42c3fe8b21ad27d33ebce9df0.png)








![5^x \approx 5^{1.732} =5^{433/250}=\sqrt[250]{5^{433}} \approx 16.241](http://upload.wikimedia.org/math/c/0/9/c09a8e4fe72ee9e5630b6ca35e726d49.png)


No comments:
Post a Comment